Examine Pre-Built Model
The top-level contents of this model are shown in Figure 1. It contains two blocks - a Ball Model and a TimeDataPlotter. The Ball Model is an instance of the FSM-Hierarchical found in the FSM library, but renamed. If you execute the model, you should see a plot like the one in Figure 6. The continuous dynamics correspond to the times when the ball is in the air, and the discrete events correspond to the times when the ball hits the surface and bounces.

Figure 1: Top-level of the Bouncing Ball Example
If you look inside the Ball Model, you will see Figure 2. Figure 2 shows a state-machine editor, which has a slightly different toolbar and a significantly different library at the left. The circles in Figure 2 are states, and the arcs between circles are transitions between states. The FSM-Hierarchical has modes, which represent regimes of operation. Each mode is represented by a state in a finite-state machine.
The state machine in Figure 2 has three states - init, free, and stops. The init state is the initial state, which is set as shown in Figure 3. The free state represents the mode of operation where the ball is in free fall, and the stop state represents the mode where the ball has stopped bouncing.
At any time during the execution of the model, the modal model is in one of these three states.
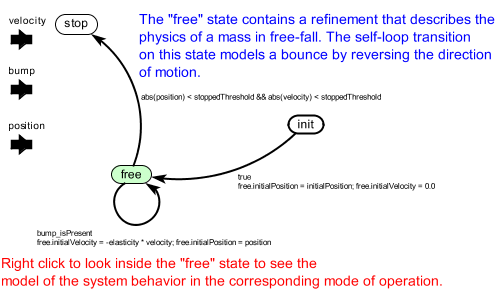
Figure 2: Inside the Ball Hierarchy of Figure 1
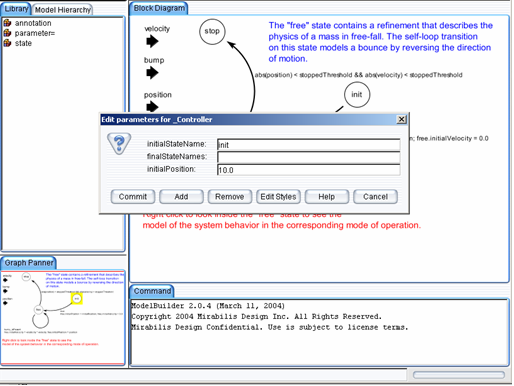
Figure 3: Initial and final states are specified by right-click on the canvas and select "Configure"
When the model begins executing, it is in the init state. During the time the model is in a state, the behavior of the model is specified by the refinement of the state. The refinement can be examined by looking inside the state. As shown in Figure 4, the init state has no refinement. Consider the transition from init to free as shown in Figure 4. It is labeled as follows:
true
free.initialPosition = initialPosition; free.initialVelocity = 0.0
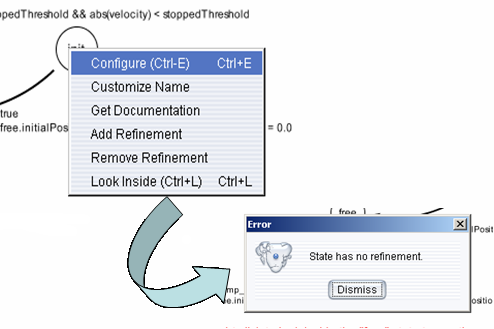
Figure 4: A state may or may not have a refinement, which specified the behavior of the model while the model is in that state. In this case, the init has no refinement.
The first line is a guard, which is predicate that determines when the transition is enabled. In this case, the transition is always enabled, as the predicate has value true. Thus, the first thing this model does is to take this transition and change modes to free. The second line specifies a sequence of actions, which in this case set parameters of the destination mode free.
If you look inside the free state, you see the refinement shown in Figure 5. This model represents the laws of gravity, which state that an object of any mass will have an acceleration of roughly -10 meters/second2 (roughly). The acceleration is integrated to get the velocity, which is, in turn, integrated to get the vertical position.
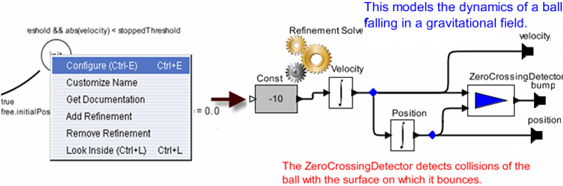
Figure 5: The refinement of the free state, shown here, is a continuous-model representing the laws of Gravity.
In Figure 5, a ZeroCrossingDetector actor is used to detect when the vertical position of the ball is zero. This results in production of an event on the (discrete) output bump. Examining Figure 2, you can see that this event triggers a state transition back to the same free state, but where the initialVelocity parameter is changed to reverse the sign and attenuate it by the elasticity. This results in the ball bouncing, and losing energy.
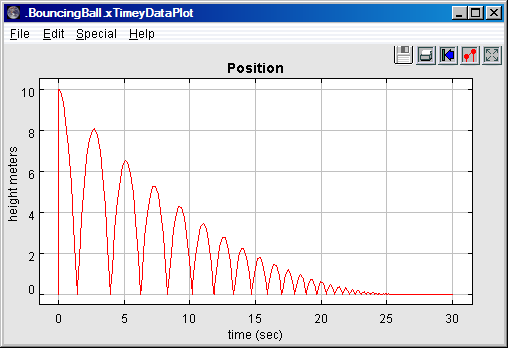
Figure 6: Result of running the bouncing ball model without the stop state.
As you can see from Figure 2, when the position and velocity of the ball drop below a specified threshold, the state machine transitions to the state stop, which has no refinement. This results in the model producing no further output.
The bouncing ball model of Figures 1 and 2 illustrates an interesting property of hybrid system modeling. The stop state, it turns out, is essential. Without it, the time between bounces keeps decreasing, as does the magnitude of each bounce. At some point, these numbers get smaller than the representable precision, and large errors start to occur. If you remove the stop state from the FSM, and re-run the model, you get the result shown in figure 6. The ball, in effect, falls through the surface on which it is bouncing and then goes into a free-fall in the space below.
The error that occurs here illustrates some fundamental pitfalls with hybrid system modeling. The event detected by the ZeroCrossingDetector actor can be missed by the simulator. This actor works with the solver to attempt to identify the precise point in time when the event occurs. It ensures that the simulation includes a sample time at that time. However, when the numbers get small enough, numerical errors take over, and the event is missed.
A related phenomenon is called the Zeno phenomenon. In the case of the bouncing ball, the time between bounces gets smaller as the simulation progresses. As simulator attempts to capture every bounce event with a time step, we could encounter the problem where the number of time steps becomes infinite over a finite time interval. This makes it impossible for time to advance. In fact, in theory, the bouncing ball example exhibits this Zeno phenomenon. However, numerical precision errors take over, as the simulator cannot possibly keep decreasing the magnitude of the time increments.
The lesson is that some caution needs to be exercised when relying on the results of a simulation of a hybrid system. Use your judgment.