DAG One Way Example; note no return to prior state a,b,c,d:
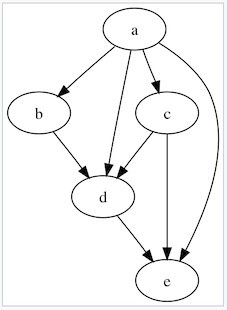
A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph, each edge has an orientation, from one vertex to another vertex. A path in a directed graph is a sequence of edges having the property that the ending vertex of each edge in the sequence is the same as the starting vertex of the next edge in the sequence; a path forms a cycle if the starting vertex of its first edge equals the ending vertex of its last edge. A directed acyclic graph is a directed graph that has no cycles.
A vertex v of a directed graph is said to be reachable from another vertex u when there exists a path that starts at u and ends at v. As a special case, every vertex is considered to be reachable from itself (by a path with zero edges). If a vertex can reach itself via a nontrivial path (a path with one or more edges), then that path is a cycle, so another way to define directed acyclic graphs is that they are the graphs in which no vertex can reach itself via a nontrivial path.
Directed Acyclic Graphs or Task Graphs; states and transitions; mathematical properties:
(1) Reachability, Transitive closure or reduction
(2) Topological ordering
(3) Combinatorial enumeration
(4) Families of Graphs
Computer-related problems task graphs can address:
(1) Topological sorting or pattern recognition
(2) Graphical State construction or simplification
(3) Transitive closure or reduction (1 level)
(4) Maximum flow cases
(5) Path algorithms
Task graphs can be used for scheduling, data networks, publications, data version history, data compression, or image classification in conjunction with AI. One might also include state diagrams or software flow task graphs. The goal of these two task graph scenarios is to simplify the flow or number of states, i.e. reduction, while maintaining the same functionality.
Web: https://en.wikipedia.org/wiki/Directed_acyclic_graph